Prüfung: Informationstechnik
Termin: Mittwoch,
17. Juli 2002
08:30 – 10:30
Prüfer: Prof. J. Walter
Hilfsmittel: beliebig
Name: _________________________
Vorname: _________________________
Bemerkung: _________________________
bitte keine rote Farbe verwenden
(nicht ausfüllen) !
|
Aufgabe |
mögl.
Punkte |
erreichte
Punkte |
|
1 |
10 |
|
|
2 |
11 |
|
|
3 |
10 |
|
|
4 |
10 |
|
|
5 |
9 |
|
|
|
|
|
|
|
|
|
|
Gesamt |
50 |
|
|
|
|
|
|
|
Note |
|
Bearbeiten
Sie die Aufgaben nur, falls Sie keine gesundheitlichen Beschwerden haben.
Viel
Erfolg
Bemerkung:
Sie können die Vorder- und Rückseite benutzten. Es werden nur die auf
den Prüfungsblättern vorhandenen oder fest mit den Prüfungsblättern verbundenen
Ergebnisse gewertet.
1. Gauß'sches Prinzip
der kleinsten Fehlerquadrate (10 Punkte)
Die Funktion ![]() soll im Bereich
soll im Bereich ![]() optimal durch eine Gerade
optimal durch eine Gerade
![]() angenähert werden.
angenähert werden.
a) Bestimmen Sie die Gleichung der Geraden
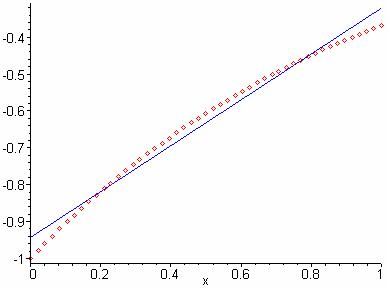
b) Skizzieren Sie das Ergebnis
Lösung:
![]()
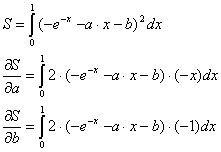
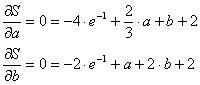
![]()
Lösung mit Maple:
diff(int( ((-exp(-x))-(a*x+b))^2, x=0..1 ),a);
-4 exp(-1) + 2/3 a + b +
2
> diff(int( ((-exp(-x))-(a*x+b))^2, x=0..1 ),b);
-2 exp(-1) + a + 2 b + 2
>
>
> solve(
-4*exp(-1)+2/3*a+b+2=0, b );
3/4 exp(2) - 12/5 a - 3/4
> solve(
-2*exp(-1)+a+2*b+2=0, a );
>
2 exp(-1) - 2 b - 2
> solve(
-4*exp(-1)+2/3*(2*exp(-1)-2*b-2)+b+2=0, b );
-8 exp(-1) + 2
> solve(
-2*exp(-1)+a+2*(-8*exp(-1)+2)+2=0, a );
>
18 exp(-1) - 6
>
> plot([-exp(-x),
(18*exp(-1)-6)*x+(-8*exp(-1)+2)], x=0..1, color=[red,blue],
style=[point,line]);
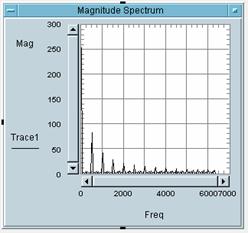
2. DFT (11 Punkte)
Eine Rampenfunktion
(Amplitudenwerte +1, -1) mit der Frequenz 100 Hz wird mit der Blockgröße N=10
abgetastet. Die Messzeit ist 20ms.
a)
2P Tragen Sie
die Abtastwerte in die Zeichnung und die Werte in die Tabelle ein.
b)
5P Berechnen
Sie aus den Abtastwerten die DFT für m=0, m=2, m=4.
c)
1P Wie groß
ist die Grundfrequenz für m=1?
d)
1P Wie groß
ist die Amplitude für m=1? Ohne Berechnung, jedoch mit Begründung.
e)
2P Welcher
prinzipielle Fehler wird bei dieser Abtastung gemacht?
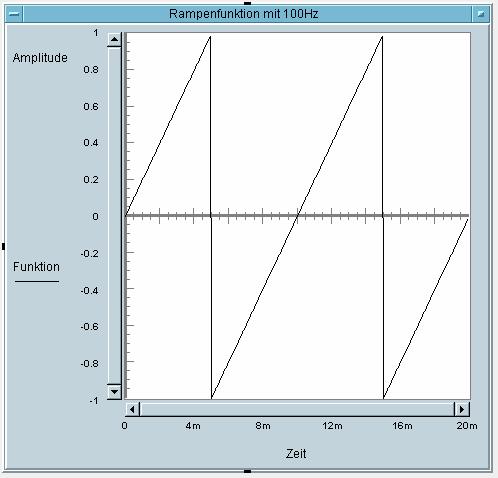
Lösung a :
|
n= |
f(n) |
|
0 |
0 |
|
1 |
0,4 |
|
2 |
0,8 |
|
3 |
-0,8 |
|
4 |
-0,4 |
|
5 |
0 |
|
6 |
0,4 |
|
7 |
0,8 |
|
8 |
-0,8 |
|
9 |
-0,4 |
Lösung b :
Mit der Formel
![]()
und den Werten für N=10, ergeben sich für die jeweiligen Ergebnisse:
|
m-te
Harmonische |
Amplitude |
|
0 = Mittelwert |
0 |
|
1. |
0 |
|
2. |
0,68 |
|
3. |
0 |
|
4. |
0,42 |
Lösung c :
50 Hz
Lösung e :
Für m=1 ist die Amplitude 0, da die Frequenz 50Hz =
tiefste Signalfrequenz nicht als Signal vorkommt.
Lösung f :
Aliasing : Im Signal sind Frequenzanteile welche
größer als ½ fABTAST sind.
Lösung auch mit HP VEE V3.2 aber Vorsicht, Faktor 2/N
berücksichtigen !
3 DGL - Übertragungsfunktion -
Systemantwort (10 Punkte)
Erstellen
Sie für die nachfolgende Schaltung die Übertragungsfunktion.

Schaltung mit R,L
und C
a) Erstellen
Sie die Übertragungsfunktion G(s)
b) Erstellen
Sie die Differentialgleichung für den Zeitbereich ( System ist am Anfang in
Ruhe)
c) Bestimmen
Sie die Impulsantwort für die normierten Werte R=1, C=1, L=1
d) Skizzieren
Sie die Impulsantwort für t=0 bis 15
Lösung
Aufgabe 3a
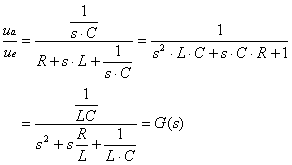
Lösung b
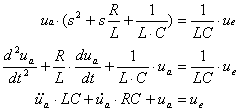
Lösung Aufgabe c
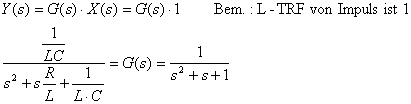
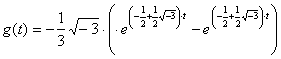
with(inttrans):
>
invlaplace(1/(s^2+s+1), s, t);
- 1/3 sqrt(-3)
(exp((-1/2 + 1/2 sqrt(-3)) t) - exp((-1/2 - 1/2 sqrt(-3)) t))
> plot(-1/3*sqrt(-3)*(exp((-1/2+1/2*sqrt(-3))*t)-exp((-1/2-1/2*sqrt(-3))*t)),t=0..15);
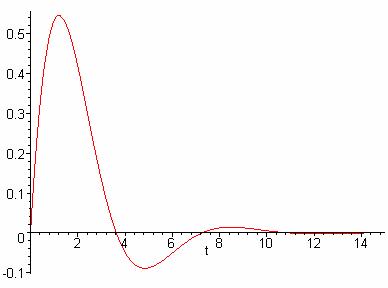
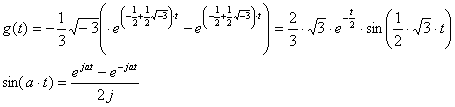
4 FIR-Filter (10 Punkte)
Ein Bandpaß
mit den Grenzfrequenzen fgoben = 200Hz und fgunten=150Hz ist als FIR-Filter für
N=3 zu entwerfen. Die Abtastfrequenz beträgt fa=5 kHz.
a) Berechnen
Sie die Filtergleichung für das FIR-Filter
![]()
b) Berechnen und skizzieren Sie die Antwort des FIR-Filters auf einen Impuls der Breite von 10 Abtastwerten.
Lösung:
![]()
![]()
|
-3 |
0,01577972 |
a-3 |
|
-2 |
a-2 |
|
|
-1 |
a-1 |
|
|
0 |
a0 |
|
|
1 |
a+1 |
|
|
2 |
a+2 |
|
|
3 |
a+3 |
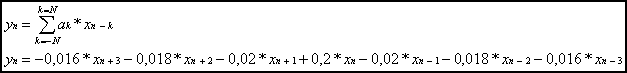
Berechnung mit Excel:
|
0 |
0 |
|
0 |
0,016 |
|
0 |
0,034 |
|
0 |
0,053 |
|
1 |
0,073 |
|
1 |
0,093 |
|
1 |
0,111 |
|
1 |
0,111 |
|
1 |
0,111 |
|
1 |
0,111 |
|
1 |
0,111 |
|
1 |
0,095 |
|
1 |
0,077 |
|
1 |
0,058 |
|
0 |
0,038 |
|
0 |
0,018 |
|
0 |
0 |
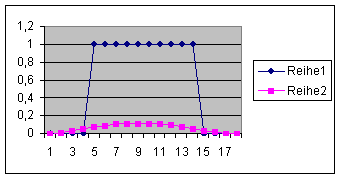
Reihe 1 = Eingang FIR-Filter
Reihe 2 = Ausgang FIR-Filter
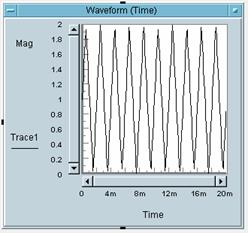
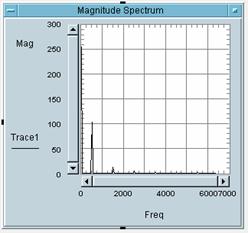
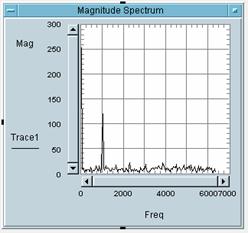
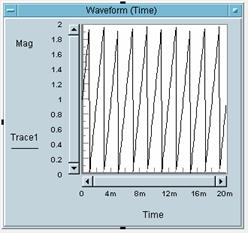
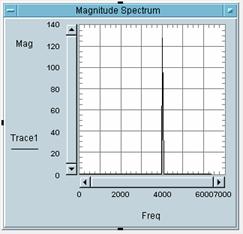
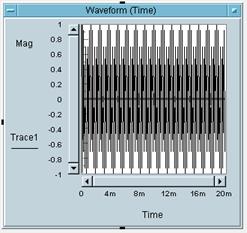
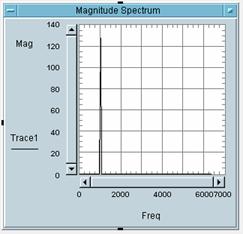
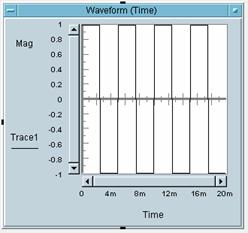
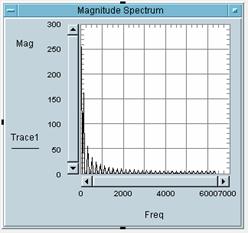
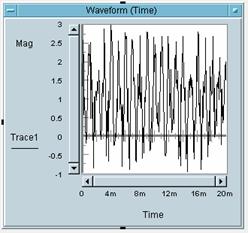
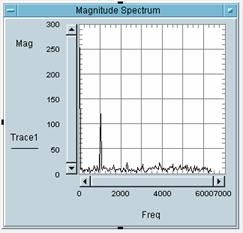
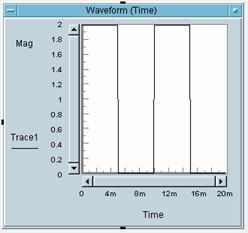
5 Bitte weisen Sie die
Zahlen der Bilder den Buchstaben des entsprechenden Bildes zu:
|
|
|
|
|
|
|
|
|
Bild 1 gehört zu Buchstabe: _C_
Bild 2 gehört zu Buchstabe: _A_
Bild 3 gehört zu Buchstabe: _B_
Bitte weisen Sie die Zahlen der Bilder den Buchstaben des entsprechenden Bildes zu:
|
|
|
|
|
|
|
|
|
Bild 1 gehört zu Buchstabe: _C_
Bild 2 gehört zu Buchstabe: _B_
Bild 3 gehört zu Buchstabe: _A_
Bitte weisen Sie die Zahlen der Bilder den Buchstaben des entsprechenden Bildes zu:
|
|
|
|
|
|
|
|
|
Bild 1 gehört zu Buchstabe: _A_
Bild 2 gehört zu Buchstabe: _B_
Bild 3 gehört zu Buchstabe: _C_
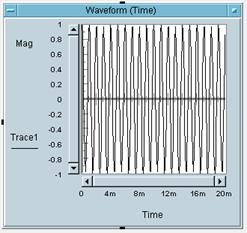
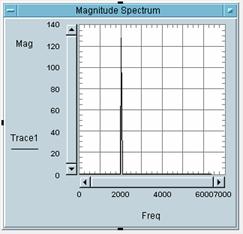
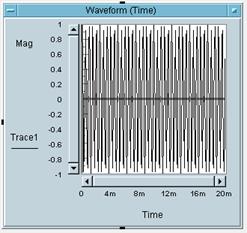
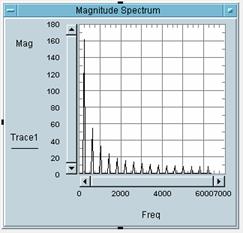 Bild
C
Bild
C