grenze
grenze
Normal
Normal
Messwerte
Messwerte
 |
|||
 |
|||
| xg |
| xg - 2 * sg |
| xg + 2 * sg |
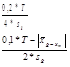
| HS KA | Messsystemanalyse | Seite 1 / 1 | Einzelwerte | obere Spez.- grenze |
untere Spez.- grenze |
obere Grenze Normal |
untere Grenze Normal |
obere Grenze Messwerte |
untere Grenze Messwerte |
||||||||||||||||||||||||||||
| FE_WS16_17_Sensorarray | Verfahren 1: Cg / Cgk - Studie | -437,784135 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||
| -437,784135 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,784135 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,784135 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| Akt. Dat.: | 24.04.2017 | Bearb.Name: | Tim Schanz | Abt./Kst./Prod.: | HS KA | Prüfort: | Halle 1 kurz | -437,784135 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| Prüfmittel | Normal | Merkmal | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| Bezeichnung: | LeddarM16 | Bezeichnung: | S16 | Bezeichnung: | Verfahren 1 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||
| Nummer: | 1 | Nummer: | 1 | Segment: | 16 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||
| Auflösung: | 1 | Istwert: | 1000 | Nennmaß: | 1000 | OSG: | 1050 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||
| Prüfgrnd.: | Abnahme | Einheit: | mm | Einheit: | mm | USG: | 950 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||
| Offset | 35 | WinkelFehler | 402,7841352 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||
| Bemerkung: | Beispiel für | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||
|
-437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||||||||||
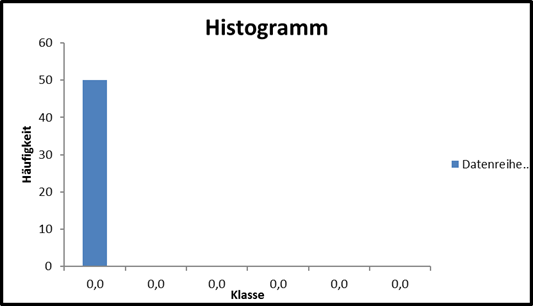
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | Klassen | Häufigkeit | |||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | #DIV/0! | 50 | |||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | Min | -437,8 | #DIV/0! | 0 | |||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | Max | -437,8 | #DIV/0! | #NV | |||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | Diff | 0,0 | #DIV/0! | #NV | |||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | kBreite | 0,0 | #DIV/0! | #NV | |||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | #DIV/0! | #NV | |||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | #NV | ||||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | Summe : | #NV | |||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
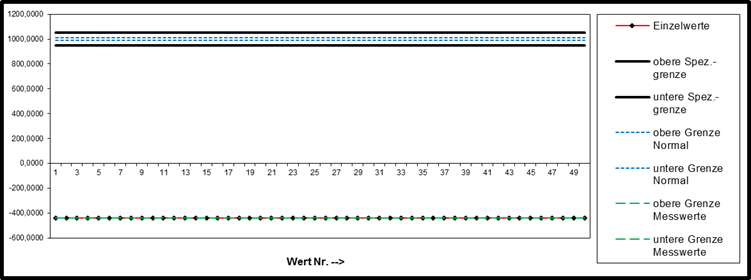
| Einzelwerte | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||||||||||
| 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 | 41 | 46 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||
| -437,7841 | -437,7841 | -437,7841352 | -437,7841 | -437,7841 | -437,78414 | -437,7841 | -437,7841 | -437,78414 | -437,7841352 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||
| -437,7841 | -437,7841 | -437,7841352 | -437,7841 | -437,7841 | -437,78414 | -437,7841 | -437,7841 | -437,78414 | -437,7841352 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||
| -437,7841 | -437,7841 | -437,7841352 | -437,7841 | -437,7841 | -437,78414 | -437,7841 | -437,7841 | -437,78414 | -437,7841352 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||
| -437,7841 | -437,7841 | -437,7841352 | -437,7841 | -437,7841 | -437,78414 | -437,7841 | -437,7841 | -437,78414 | -437,7841352 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||
| -437,7841 | -437,7841 | -437,7841352 | -437,7841 | -437,7841 | -437,78414 | -437,7841 | -437,7841 | -437,78414 | -437,7841352 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
| Spezifikationswerte | Gemessene Werte | Statistische Werte | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||||||||
| xm | 1000,0000 | mm |
|
-437,7841352 | mm | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||
| xm - 0,1*T | 990,0000 | mm | xmin. | -437,7841 | mm |
|
-437,7841 | mm | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||
| xm + 0,1*T | 1010,0000 | mm | xmax. | -437,7841 | mm |
|
-437,7841 | mm | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||
| 0,2 * T | 20,0000 | mm | R | 0 | mm | 4 * sg | 0,00000 | mm | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||
| T | 100,0000 | mm | nges. | 50 | Teile | sg | 0,000000 | mm | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||
| -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||||
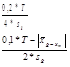
|

|
Messsystem fähig für T bis | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||||||||
| Cg = | = | ############ | ######### | ######### | Tmin/Cg = | 0,0000 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||||
| ######### | ######### | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | |||||||||||||||||||||||||||||
| Cgk = | = | ############ | 14,285714 | 85,71 | Tmin/Cgk = | -14377,8414 | -437,7841 | 1050,0000 | 950,0000 | 1010,0000 | 990,0000 | -437,7841 | -437,7841 | ||||||||||||||||||||||||
| Auflösung | = | 1,00% | Tmax. Aufl. = | 20,0000 | |||||||||||||||||||||||||||||||||
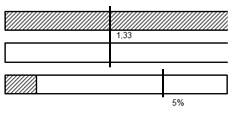
| Hinweise: | 1.) | Auflösung ist ausreichend ! (Auflösung ist kleiner oder gleich 5% !) | |||||||||||||||||||||||||||||||||||
| 2.) | Meßgerät ist besser zu zentrieren ! (Cg ist noch kleiner als die Mindestbedingung 1,33 !) | ||||||||||||||||||||||||||||||||||||
| Beschreibung: | m = Master (Normal) | g = Gage (Prüfmittel) | |||||||||||||||||||||||||||||||||||
| Datum: | ________ | Unterschrift: | __________________ | Abteilung: | __________________ | ||||||||||||||||||||||||||||||||