3 Leistungsauslegung

Die gezeigte Leistungsauslegung beruht auf der Strahl- bzw. Stromfadentheorie nach Bernulli. Die in Abbildung 3 zu sehende Skizze zeigt einen idealen Rotor, der als kreisförmiges Kontinuum in der Lage ist, Luft nach unten zu Beschleunigen.

Abbildung 3: Schematische Darstellung Strahltheorie

Der nötige Schub entsteht durch die Beschleunigung der durch den Rotor strömenden Luftmassen. Dabei entsteht oberhalb des Rotors ein Unterdruck und unterhalb ein Überdruck. Der resultierende Druckunterschied wirkt auf die Rotorkreisfläche und erzeugt den Schub.

Entsprechend der obigen Skizze lässt sich die folgende Gleichung herleiten, um die nötige Leistung eines idealen Rotors bei gefordertem Schub zu berechnen:

 

(3.1)

Auf eine detaillierte Herleitung der Gleichung wird hier verzichtet. Sie kann in „Flugmechanik der Hubschrauber“ von Walter Bittner nachgelesen werden.

3.1       Leistungsbedarf im Schwebeflug

Für die Berechnung gelten die folgenden Randbedingungen:

 

Tabelle 3‑1:Leistunsdaten

Gesamtgewicht [kg]:

3

Rotordurchmesser [m]:

0,254

Wirkungsgrad (Schwebegüte Rotor):

1

Anzahl Rotoren:

6

Luftdichte 20°C [kg/m^2]:

1,293

Gewichtskraft [N]:

29,43

Rotorkreisfläche gesamt [m^2]

0,30402449

 

Ideale benötigte Gesamtleistung:

 

(3.2)

Dies entspricht einer idealen Leistung pro Rotor von 30,01 W.

 

Abzug Gütegrad Luftschraube/ Schwebegüte

Ein realer Rotor besitzt im Schwebeflug die folgenden Verluste:

 

Tabelle 3‑2: Verlsutquellen

Profilwiderstand

20-30 %

Ungleichförmiger Durchfluss

5-7 %

Restdrall im Luftstrom

2 %

Blattspitzenverluste

2-4 %

 

Der Wirkungsgrad eines für Multikopter eigesetzten Rotors liegt im Schnitt bei ca. 0,6. Unter dieser Berücksichtigung beträgt die benötigte Motorleistung des einzelnen Motors:

 

(3.3)

 

Um die elektrische Eingangsleistung des Motors zu bestimmen, müssen noch der Motorwirkungsgrad und der des Reglers miteinbezogen werden:

 

 

(3.4)

 

3.2       Simulation mit Hilfe von JavaProp

JavaProp ist ein java-basierendes Freeware Tool zur Auslegung und Berechnung von Luftschrauben. Die Berechnung erfolgt nach dem Verfahren der Blattelementmethode.

Der Arbeitsablauf ist in Abbildung 4 zusammengefasst:

Für die Simulation wird  zunächst die ausgewählte Luftschraube vermessen und die ermittelten Koordinaten in JavaProp eingetragen. Die Vermessung erfolgt durch Angabe der Geometrie an vier Schnitten entlang der Luftschraube. Durch die Auswahl eines Profils (hier Ara D6% für Modellschrauben), werden die restlichen Koordinaten durch das Programm interpoliert und somit ein nahezu identisches Luftschraubenprofil erzeugt. Das nun digitalisierte Profil dient als Basis für die Simulation und kann darüber hinaus als CAD Modell exportiert werden.

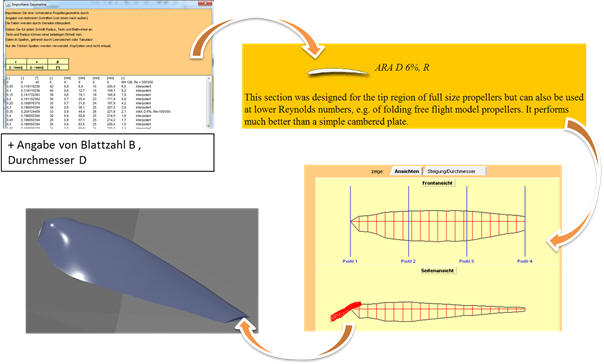
Abbildung 4: Digitalisierung des Propellerprofils

3.3       Verifizierung anhand eines Leistungsprüfstands

Damit die aufgezeigte Leistungsauslegung unter Realbedingungen verifiziert werden kann, wird ein Prüfstand aufgebaut.

Ziel des Prüfstands ist die Ermittlung des resultierenden Schubs und die damit verbundene elektrische Leistungsaufnahme. Als Motor- Luftschraubenkombination wird eine 10x5,5“  in Verbindung mit einem Hacker A40 Motor verwendet.

3.3.1        Aufbau

Der Leistungsprüfstand in Abbildung 4 besteht aus einem mittig drehbar gelagertem Hebelarm (1), an dessen Ende der Brushless Motor mit Luftschraube (2) montiert ist. Das andere Ende liegt auf eine Waage (3) auf und überträgt somit eins zu eins den an der Luftschraube erzeugten Schub.

Bei der Versuchsdruchführung wird die Spannung direkt am Lipo mit Hilfe eines Multimeters (4) gemessen. Der Strom zwischen Lipo und Regler wird mit einer Strommesszange (5) gemessen. Zusätzlich wird die Propellerdrehzahl mit Hilfe eines optischen Sensors (6) gemessen. Das PWM Signal für den Motorregler wird über ein STM Discovery Board (7) erzeugt. Die Stellgröße kann dabei Schrittweise von 0 – 100% variiert werden.

 

 

Abbildung 5: Leistungsprüfstand

In Abbildung 5 sind Schub, elektrische Leistung, die mit der Strahltheorie berechnete Leistung sowie der jeweils resultierende Gesamtwirkungsgrad über der Drehzahl gezeigt.

 

3.4       Auswertung und Vergleich

Im folgenden Kapitel werden die Berechnung mit Strahltheorie sowie die Simulationsergebnisse aus JavaProp mit den am Prüfstand gemessenen Ergebnissen und Werten verglichen und ausgewertet.

Abbildung 7 zeigt die Gegenüberstellung der Ergebnisse der Strahltheorie mit denen aus der Simulation mit JavaProp.

 

Abbildung 6: Leistungsbedarf Strahltheorie und JavaProp

Grundsätzlich weicht die die Simulationskurve von JavaProp (grün) gravierend von der der Strahltheorie (blau) ab . Der Grund hierfür liegt darin, dass die Strahltheorie nur einen idealen Rotor betrachtet und jegliche Verluste vollständig vernachlässigt. Die Strahltheorie kann somit nur in Verbindung mit einem Propellerwirkungsgrad verwendet werden. Für den Vergleich wird somit ein Wirkungsgrad von 0,6 angenommen wodurch ein nahezu identischer Verlauf (rot) erzielt wird. Somit bestätigt die Simulation die analytischen Berechnungen.

In Abbildung 7 erfolgt abschließend der Vergleich zwischen Simulation und Prüfstand.

 

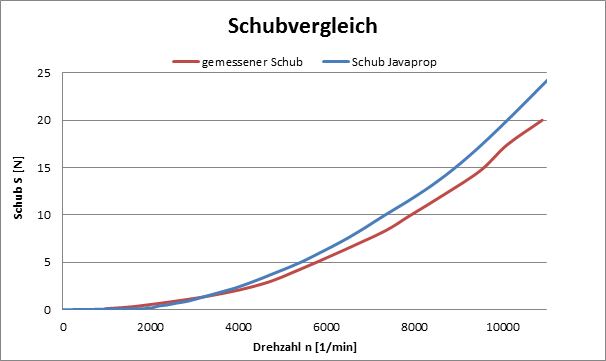
Abbildung 7: Schubvergleich von JavaProp und Prüfstand

Grundsätzlich sind ähnlicher Verläufe der beiden Kurven zu beobachten, so dass der Prüfstand die Gültigkeit der Simulation bestätigt. Die dennoch erkennbaren Abweichungen resultieren aus den nicht berücksichtigten Querströmungen von JavaProp durch die Verwendung eines 2-dimensionalen Verfahrens. Dies erklärt den leicht höheren Verlauf der simulierten Schubkurve. Des weiteren unterscheidet sich das digitalisierte Blattprofil durch Messungenauigkeiten vom realen Profil.

Somit lassen sich aus den Ergebnissen aus der analytischen Berechnung, der Simulation sowie den aus der Messung gewonnen Erkenntnissen eine geeignete Motorauswahl durchführen.

Die folgende Abbildung zeigt die elektrisch gemessene Leistung über der Drehzahl und Schub. Entscheiden für die Motorauswahl ist der Leistungsbedarf bei einem Schub von 500g, da dies den Anforderungen an den Schwebeflug des Hexakopter entspricht.

Abbildung 8: Leistungsbedarf im Schwebeflug bei 500g Schub

Die gemessene elektrische Leistung liegt bei 85W und einem Wirkungsgrad von 32%. Für die Motorauswahl wird folgende Faustformel verwendet:

PMotor = PSchweben * 2,5 = 85 W * 2,5 = 212 W

Da bei den Motoren auf die Firma Hacker zurückgegriffen werden soll, wird ein Multikoptermotor der Baureihe A30 verwendet:

A30 52S UAV           200W Dauerleistung / 250 W Spitzenleistung

 

3.5       Leistungsbedarf im Steigflug

 

Entsprechend der Strahltheorie, ergibt sich die notwendige Steigleistung je Motor nach folgender Formel:

 

(3.5)

Der Quotient  ergibt sich aus:

(3.6)

 

Dabei ist

 

(3.7)

  

und  die Steiggeschwindigkeit des Kopters. Die Steiggeschwindigkeit wird mit 6 m/s angenommen.

Somit ergibt sich folgende Rechnung:

 

 

 

(3.8)

 

 

Die nötige ideale Steigleistung eines Motors ergibt sich somit zu:

(3.9)

 

(3.10)

 

Die tatsächlich nötige Steigleistung beläuft sich auf:

 

(3.11)

 

Mit Hilfe des berechneten und am Prüfstand ermittelten Leistungsbedarfs und der Vorgabe einen Motor der Firma Hacker auszuwählen, wird der Motor A30 52S UAV ausgewählt (siehe Abbildung 7).

 

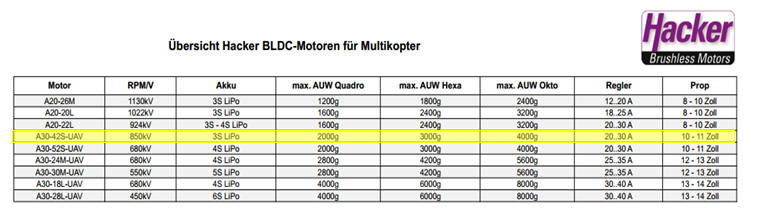
Abbildung 9: Überischt Hacker Brushless Motoren

Der Motor ist speziell für Multikopter und für Hexakopter mit einem Abfluggewicht von 3 kg von Hacker empfohlen. Das Datenblatt des Motors befindet sich im Anhang.