|
Entlang
einer Schiene bewegendes Gewicht
Das Ziel des
Projekts ist, dass das Fahrrad nicht von selbst umfallen lässt.
Deshalb ist es wichtig zu erkennen, welche Parameter dafür wichtig
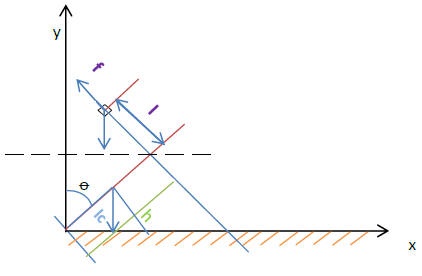
sind. In der folgenden Abbildung wird gezeigt, wie das
Koordinatensystem des Fahrrads definiert ist:
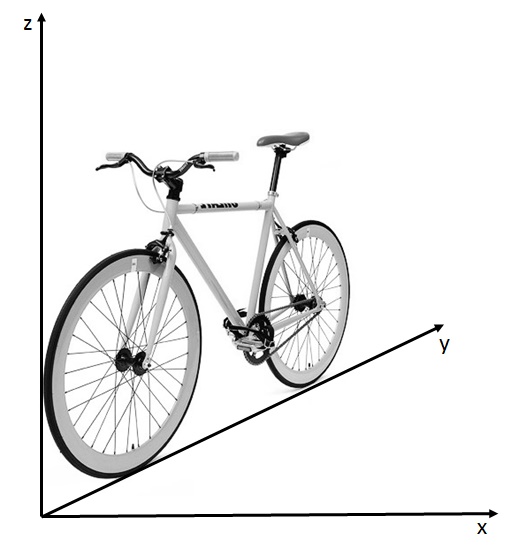
Der Winkel “Theta” (ϴ) ist der zu regelnde
Hauptausgang. Er liegt zwischen dem Fahrrad und der Ebene x-z. Das
Gewicht des Fahrrads wird “W” (Weigth) genannt, wie man im Folgenden
sehen kann:
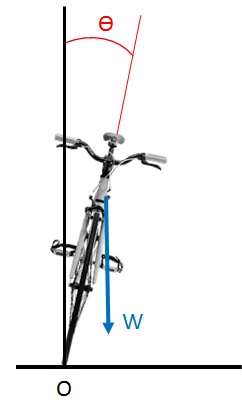
Um das Gleichgewicht des Fahrrads erreichen
zu können, muss dieser Winkel natürlicherweise zu null gehen.
Außerdem sollten einige Voraussetzungen erfüllt werden, wie zum
Beispiel, muss Theta einen Anfangswert von weniger als einen
bestimmten Winkel haben, denn sonst lässt sich niemals das System
zum gewünschten Zustand bringen. Die obengenannten
Voraussetzungen hängen von den Kräften ab, die jede Lösung erzeugen
kann.
In dieser Lösung 1 geht es um die Positionierung eine
Masse entlang einer Schiene, die senkrecht zu der Seite des Fahrrads
steht, so dass durch die Stellung des kontrollierten zusätzlichen
Gewichts ein Drehmoment geschafft werden kann, das das System zum
Stehen bringt.
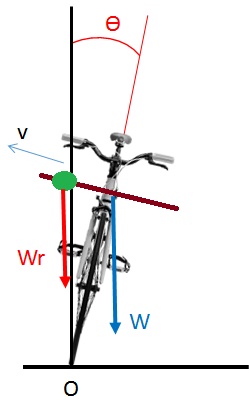
Die Länge der Schiene oder das Gewicht der
Masse sind vom Gewicht und Form des zu balancierenden Fahrrads
abhängig, aber man kann immer noch schon bemerken, dass je länger
die Schiene ist oder je schwerer die Masse ist, desto breiter kann
der zu regelnde Winkel sein.
Trotzdem kann die Schiene nicht
nur wegen des ästhetischen Aspekt zu lang sein, sondern auch weil
dann das Fahrrad nicht neigen könnte. Weiterhin wenn das Gewicht der
Masse zu schwer wäre, konnte es von einem Antrieb entlang der
Schiene nicht transportiert werden.
In dieser Lösung gibt es
auch die Möglichkeit einige Varianten zu machen. Beispielsweise
könnte man zwei zu regelnde Gewichte anwenden oder die Schiene
klappbar machen.
Modellierung des Systems:
Aus der statische
Analyse vom Grenzfall bekommt man das folgende Ergebnis:
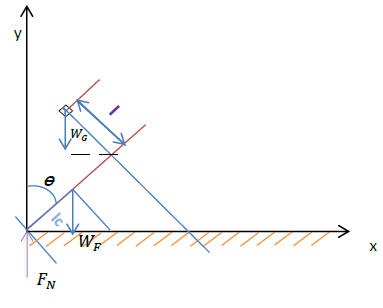 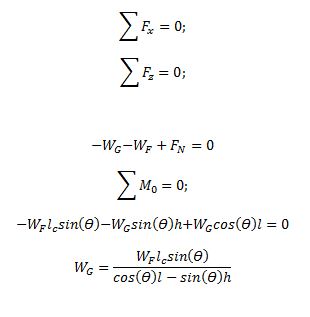
Für diese mathematische Modellierung werden
das Gewicht der bewegenden Masse als
mG
und das Gewicht des Systems vom
Fahrrad als
mf bezeichnet.
Damit ist entweder das Gewicht der
Masse oder die Länge der Schiene zu definiren, solange die andere
festgelegt ist.
Trotzdem, um das System regeln zu können,
muss man zuerst den dnamischen Modell erreichen, weil eine genauere
Darstellung nicht nur die Position sondern auch die Beschleunigungen
und Geschwindigkeiten der Bestandteile betrachten muss. Deswegen
wird der folgende Modell durchgeführt:
 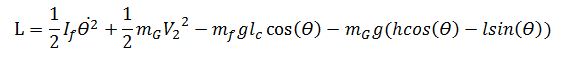
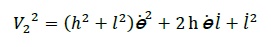
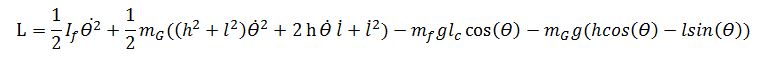
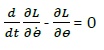
1)
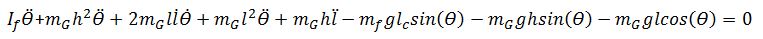
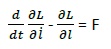
2)
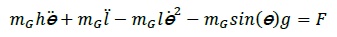
Schliesslich entstehen aus 1 und 2 die
folgende Ausdrücke, die wichtig für die Simulation und Steuerung des
Systems sind:
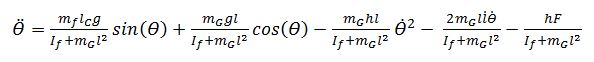
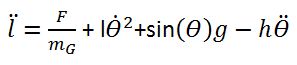
Simulation:
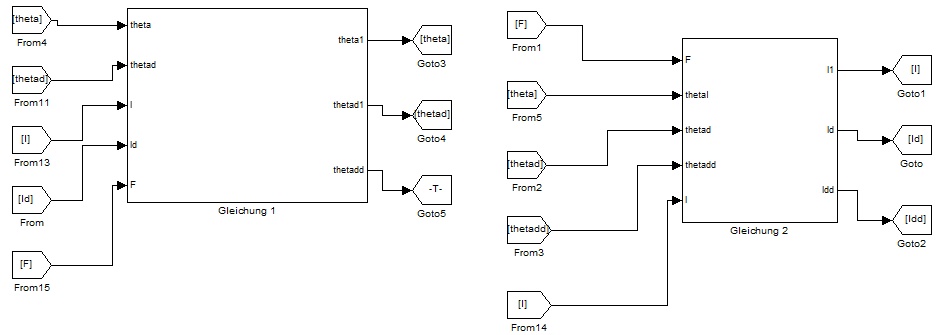
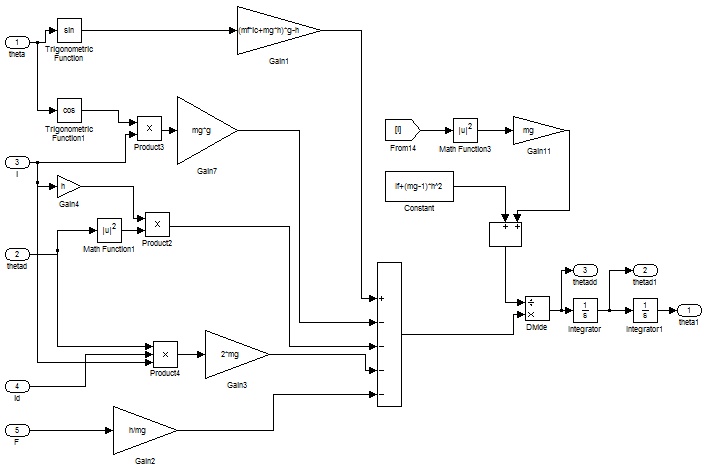
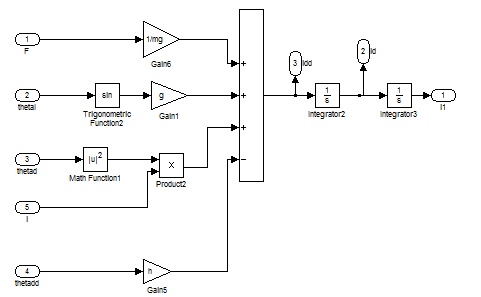
Diese Ergebnisse kommen nach Verbesserung und Korrekturen in dem
ersten Modell von FEPA. Durch die Simulation können wir sehen, wie
das Fahrrad fehlt gleichzeitig die Masse entlang des Lenkers bewegt.
Hier liegt ein Video als Beispiel:
20170613_161447.mp4
|