|
|||
|
1.
Konzept zum mechanischen Aufbau des Fahrzeugs Konzeptidee: - Fahrzeug mit niedrigem Schwerpunkt - Gewicht des Fahrzeuges soweit möglich reduzieren, um Spielraum für Regelung zu vergrößern - ABER: Ein Durchdrehen / Rutschen der Räder muss vermieden werden - Bekannter und unveränderlicher Radstand - Stift, zum Prüfen des Geradeauslaufes oder zum Malen des Haus des Nikolaus, achsmittig platzieren - Kugelrolle als drittes Rad, da damit bisher die besten Ergebnisse erziehlt wurden - Mechanischer Anschlag (s. Wiederholbarkeit) gewähltes Fahrzeugkonzept mit niedrigem Schwerpunkt Der mechanische Aufbau des Fahrzeugs hatte das Ziel, die Regelung der Encodermotoren so wenig wie möglich zu beeinflussen. Dabei wurde ein niedriger Schwerpunkt angestrebt. Dafür müssen die Motoren und der Akku des Roboters möglich niedrig verbaut werden. In der obenstehenden Abbildung ist das gewählte mechanische Konzept für das Fischertechnik-Fahrzeug zu sehen. Man kann erkennen, dass das Gewicht der Motoren und des Akkus gleichmäßig auf die Gesamtfläche des Roboters verteilt ist. Dadurch ist es ebenfalls gelungen, den Schwerpunkt des Fahrzeugs niedrig zu halten. 1.1 Konzept zum Verbessern der Wiederholbarkeit Konzeptidee: - mechanischer Anschlag in Fahrzeugkonzept integrieren (s. Abbildung) - Anfahrrampe in Software realisieren um ein Durchdrehen der Räder zu vermeiden - Haftung der Räder verbessern / Reproduzierbarkeit sicherstellen (s. Haftung) Um die Wiederholbarkeit der Versuche sicherzustellen, wurde ein mechanischer Anschlag am Ende des Fahrzeuges verbaut. Er erlaubt ein immer gleiches Aufsetzen des Fahrzeugs und soll Fehler durch schiefes Platzieren des Fahrzeugs vermeiden. Außerdem wurde in Software eine Anfahrtsrampe realisiert. Diese ermöglicht es, dass der Roboter ohne Ruck anfahren kann. Dadurch kann ein Rutschen oder Driften des Roboters im Anfahrtsprozess verhindert werden. Geplant war auch eine Verbesserung der Haftung der Räder, dies wird im nächsten Kapitel weiter betrachtet. Aufgrund der Verbesserung des Anfahrtsverhaltens durch die Anfahrtsrampe entschieden wir uns dazu, dass keine zusätzliche Strategie zur Verbesserung der Haftung der Räder notwendig ist. Außerdem gab es zwei Ansätze zur Umsetzung der Anfahrtsrampe in Software: 1. Ungeregelte Anfahrtsrampe: Bei der ungeregelten Anfahrtsrampe sollte die Motorregelung erst starten, wenn der Motor den zuvor eingestellten Sollwert erreicht hatte. Allerdings gab es hierbei große Sprünge beim Übergang von ungeregleter Rampe auf den geregelten Betrieb. Dies ist im nachfolgenden Graph zu erkennen: Ungeregelte Anfahrtsrampe mit großen Sollwertsprüngen beim Übergang zur Regelung 2. Geregelte Anfahrtsrampe: Bei einer geregelten Anfahrtsrampe ist ein deutlich besserer Übergang zwischen der Rampe und dem danach angestrebten Sollwert zu erkennen. Das Fehlverhalten des Reglers ist dabei einem Kompromiss aus Agilität und Genauigkeit geschuldet. Allerdings ist klar zu erkennen, dass eine Regelung der Anfahrtsrampe deutlich bessere Ergebnisse liefert, im Vergleich zu einer ungeregelten Anfahrt. Geregelte Anfahrtsrampe mit deutlich besserem Verhalten gegenüber einer ungeregleten Anfahrt 1.2.1. Konzept zum Verbessern der Haftung (1) Konzeptidee: - Haarspray auf Reifen aufbringen - Reifen zusätzlich aufrauen 1.2.2. Konzept zum Verbessern der Haftung (2) Konzeptidee: - Reifen mit Fahrradschlauch (oder weichen Gummibändern) überziehen - überzogenen Reifen mit Alkohol bearbeiten um weichere Reifen (mehr Haftung) zu erhalten - Reifen zusätzlich aufrauen Es wurde entschieden auf eine Verbesserung der Haftung durch oben genannnte Konzepte zu verzichten, da mit Hilfe der Anfahrtsrampe deutliche Verbesserungen im Bezug auf Rutschen und Driften des Roboters erzielt wurden. 2. Regelungskonzepte 2.1 Differenzdrehzahlregelung 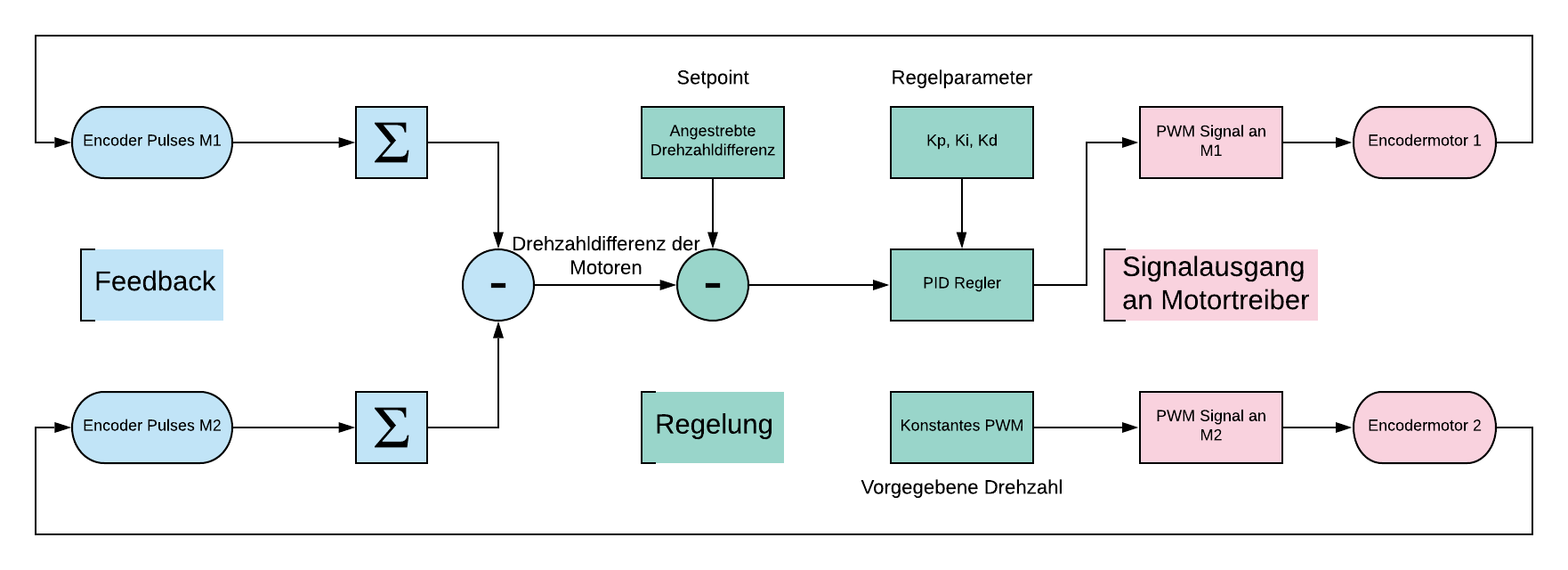 Differentdrehzahlregelungskonzept Das erste Reglerkonzept für einen Geradeauslauf wurde durch einen Differenzregler umgesetzt. Hierbei wird ein Motor mit einer vorgegebenen Geschwindigkeit beaufschlagt und der andere Motor auf die Nulldifferenz der rückgekoppelten Geschwindigkeiten geregelt. Da sich die Motoren mit diesem Konzept in jeder Lage gleich schnell drehen sollen, ist ein Geradeauslauf unumgänglich. Dieses Konzept brachte leider einige Nachteile mit sich. Die einzelnen Motoren sind mit diesem Konzept nicht mehr individuell und intuitiv bedienbar. Jede Bewegung muss in Drehzahldifferenzen ausgedrückt werden, was die gesamte Bedienbarkeit erschwert. Zudem hat sich in den ersten Versuchen gezeigt, dass es kaum möglich ist, die Drehzahldifferenz zuverlässig auszuregeln. Die Drehzahl des „führenden“ Motors ist dabei nicht genau einstellbar und unterliegt Schwankungen beispielsweise durch die Batteriespannung. Der „folgende“ Motor hinkt dem führenden Motor stehts etwas hinterher. Eine präzise Nulldifferenz der Drehzahlen ist nicht realisierbar. 2.2 Individuelle Geschwindigkeitsregelung 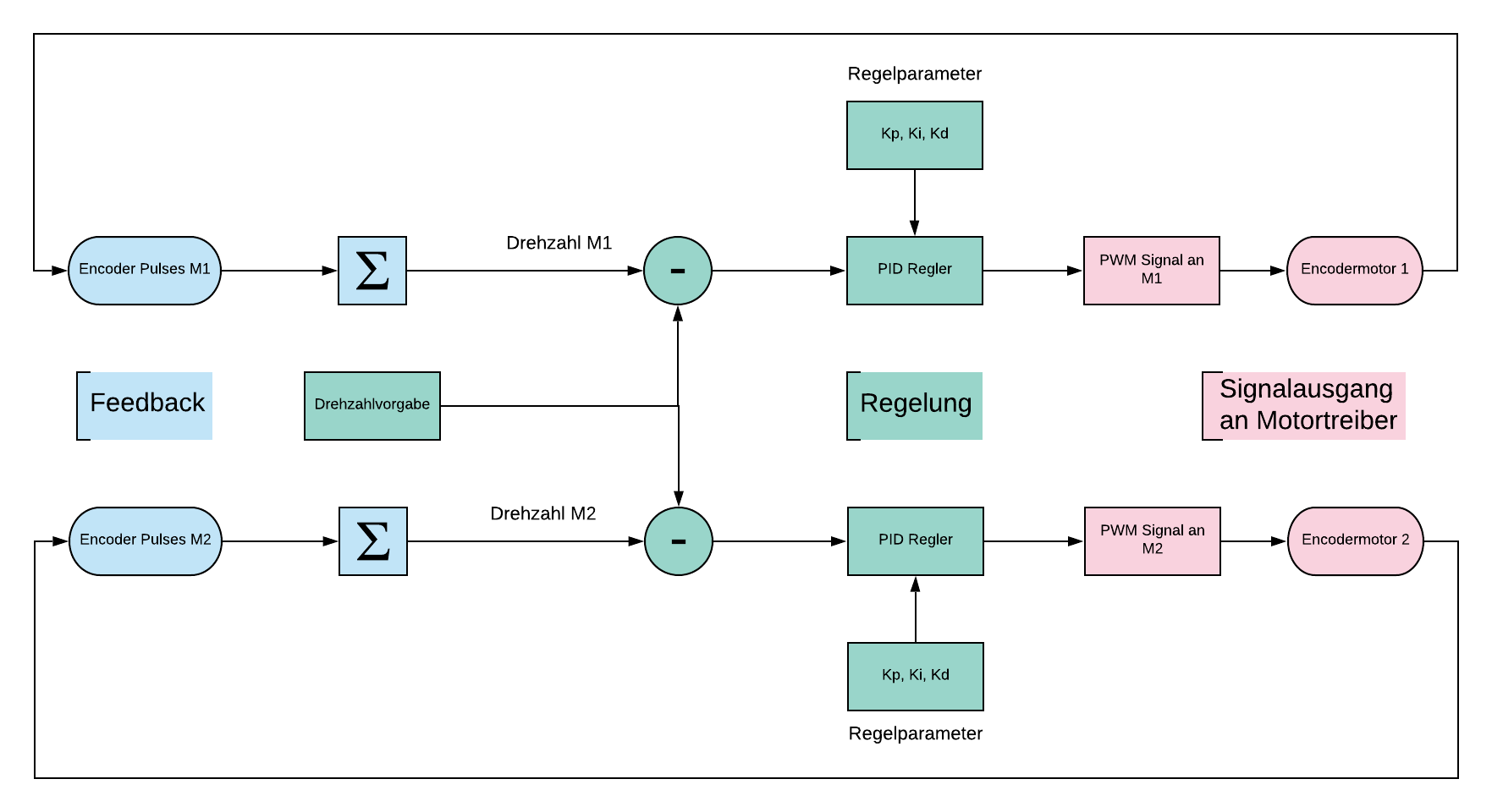 Konzept der individuellen Geschwindigkeitsregelung Im zweiten Reglerkonzept werden die Motoren einzeln mit identischen Regelkreisen geregelt. Die Parameter und der Geschwindigkeitssetpoint werden mit gleichen Werten an beide Regler übergeben. Dadurch soll ein sehr ähnliches Verhalten der beiden Regler erzielt werden. Im Versuch wurde festgestellt, dass sich die beiden Regler in der Tat sehr ähnlich verhalten. Kombiniert mit einer Anfahrtsrampe war es möglich, den Regelfehler der beiden Regler innerhalb von kleiner 0,042 Umdrehungen/s zu halten. Dies entspricht einder Encoderauflösung von +- 5 Incrementen. 2.1 Systemidentifikation und Simulation mit Matlab Simulink Konzeptidee: - Aufnahme einer Sprungantwort und bestimmen der Regelparameter - Sprungantwort wird mit Hilfe eines zusätzlichen Encoders am Ausgang der Motorwelle aufgenommen 2.1.1 Systemidentifikation
Im Folgenden wird das System identifiziert. Dies ist vorteilhaft, um
eine spätere Implementierung einer Regelung und der Einstellung der
Regelparametern zu erleichtern. Es wird die Übertragungsfunktion des
Motors identifiziert, welche mit einem PT2-Glied angenähert wird.
Für die Identifikation ist die Aufzeichnung einer Sprungantwort
nötig. Um diese aufzuzeichnen, wird ein Drehgeber auf die Motorwelle
aufgebracht und der Motor bestromt. Dabei wird die
Rotationsgeschwindigkeit über die Zeit gemessen.
Ein Elektromotor kann durch ein Verzögerungsglied zweiter Ordnung
angenähert werden. Die Übertragungsfunktion eines PT2-Glieds lautet
y(t) = K/((T1*s+1)(T2*s+1)) .
In der Abbildung 2 wurde das System
Elektromotor in Simulink aufgebaut. Bei einem Elektromotor sind die
Zeitkonstanten nur sehr gering, was zu kleinen Verzögerungszeiten
der Sprungantwort führt. Anders als in Abbildung
1, welche die beispielhafte
Sprungantwort y(t) eines PT2-Glieds darstellt, wird die Zeitskala
der Sprungantwort des Elektromotors deutlich kleiner sein. Die
Messung der Sprungantwort erfolgte im Rahmen des Projektes in einem
Zeitraum von 0,08 s.
Die Identifikation des Systems wird im Folgenden über das Gaußsche
Fehlerquadrat im Zusammenspiel mit der Matlab Optimierungsfunktion
fminsearch, welche dem Prinzip des Nelder-Mead-Algorithmus zugrunde
liegt. Da in der Messung der Sprungantwort die
Rotationsgeschwindigkeit gemessen wurde, die Regelgröße jedoch der
PWM Duty-Cycle ist, wird von Umdrehungen pro Sekunde in Duty-Cycle
umgerechnet. Hierbei hilft eine Linearisierung des PWM-Signals.
Im ersten Durchlauf der Systemidentifikation wird das Fehlerquadrat
der simulierten Kurve zur realen Kurve gebildet. Die Funktion
fminsearch erhält als Eingangsgröße die Summe des Fehlerquadrates
und gibt nach einer Iteration die Zeitkonstanten T1, T2 aus. In den
nachfolgenden Iterationen werden die neu errechneten Zeitkonstanten
als neuer Startwert verwendet und der Prozess wiederholt, solange
bis das Fehlerquadrat der gemessenen und simulierten Kurve
minimal ist. Somit kann das System adäquat identifiziert werden.
Abbildung 3
zeigt das identifizierte System. Als Anfangswert wurden die
Zeitkonstanten T1 = 0,01s und T2 = 0,01s, sowie der
Verstärkungsfaktor K = 90 gesetzt. Nach 83 Iterationen des
Algorithmus fminsearch ist der Elektromotor mit den Zeitkonstanten
T1 = 1e-4s und T2 = 0,0029s angemessen identifiziert. 2.1.2 Regelparametereinstellung Parameter für ein derartiges System können
durch empirische Methoden oder auch durch die Benutzung der
PID-Tuning App von Matlab erfolgen. Heuristische Methoden, wie
beispielsweise durch Ziegler/Nichols vorgegeben, führen zu keinem
Erfolg, da diese Methoden für Systeme mit großer Verzögerungszeit
geeignet sind. Sobald die Übertragungsfunktion identifiziert
wurde, deklariert man diese im Matlab Workspace. Parallel hierzu
wird ein Simulink-Modell benötigt, welches das identifizierte System
samt PID-Regler repräsentiert. Nun kann mit verschiedenen
Bedingungen das Verhalten des Reglers beeinflusst werden.
Beispielsweise kann die Zeit, in welcher der Regler reagiert,
eingestellt werden. Ebenso kann man zwischen robustem und
aggressivem Regelverhalten wählen.
-
Standard ( Kp = 0,016, Ki = 10,2, Kd
= -2,24e-7)
-
Schnelle Reaktionszeit ( Kp = 0,2226,
Ki = 248, Kd = 4,5e-6)
-
Aggressives Regelverhalten ( Kp =
0,016, Ki = 11,07, Kd = -2,26e-7)
-
Robustes Regelverhalten ( Kp =
0,0195, Ki = 7,6, Kd = 4,92e-6) Die von MatLab ermittelten Regelparameter wurden im Weitern im Realbetrieb untersucht. Nachfolgend die erhaltenen Resultate. 2.1.3.1 Ergebnisse "Standard" Kp = 0,016, Ki = 10,2 Kd = -2,24e-7 (wurde 0 gewählt, da vernachlässigbar gering) Reglerverhalten bei Einstellung "Standard" Die Einstellung „Standard“ beinhaltet die automatisch generierten Einstellungen aus der PID-Toolbox von MatLab ohne weitere manuelle Parametrierung. Man erkennt eine starke Schwingung des Istwerts um den Sollwert der Regelung. Betrachtet man die Anteile der Regelung sticht hier ein verhältnismäßig großer I-Anteil heraus. Dieser erkennt die Abweichung des Istwerts zum Sollwert und möchte den Fehler ausintegrieren, wobei Über- und Unterschwinger mit etwa gleicher Amplitude entstehen. Die Folge hierbei ist eine dauerhafte Schwingung des Istwerts. Dies zeigt, dass die hier gefundenen Regelparameter für das System ungeeignet sind. Eine Verbesserung könnte durch eine nachträgliche Reduktion des I-Anteils erreicht werden. 2.1.3.2 Ergebnisse "Schnelle Reaktionszeit" Kp = 0,2226, Ki = 248, Kd = 4,5e-6 (wurde 0 gewählt, da vernachlässigbar gering) Reglerverhalten bei Einstellung "Schnelle Reaktionszeit"
Diese Einstellung des Reglers bedeutet einen deutlich höheren
I-Anteil in der Regelstrecke, um Agilität zu gewährleisten. 2.1.3.3 Ergebnisse "Agressives Regelverhalten" Kp = 0,016, Ki = 11,07, Kd = 2,26e-7 (wurde 0 gewählt, da vernachlässigbar gering) Reglerverhalten bei Einstellung "Agressives Regelverhalten" Mit einer „aggressiven“ Reglereinstellung wird lediglich ein leicht höherer I-Anteil zur Regelstrecke hinzugefügt als bei Standard-Einstellungen. Auch mit diesen Einstellungen treten Schwingungen des Istwerts um den Sollwert, wie bei 2.1.3.1, auf. Das Verhalten des Reglers könnte hier ebenfalls durch eine Reduktion des I-Anteils der Strecke verbessert werden. 2.1.3.4 Ergebnisse "Robustes Regelverhalten" Kp = 0,0195, Ki = 7,6, Kd = 4,92e-6 (wurde 0 gewählt, da vernachlässigbar gering) Reglerverhalten bei Einstellung "Robustes Reglerverhalten"
„Robustes Regelverhalten“ beschreibt eine Einstellung, mit welcher
Störungen angemessen ausgeglichen werden können. 2.1.4 Berechnete Regelparameter Aus der oben durchfegührten Systemidentifikation wurden die Zeitkonstanten T1 = 1e-4s und T2 = 0,0029s ermittelt. Außerdem wurde zuvor der Proportionalfaktor K = 90 ermittelt. Mit diesen Zeitkonstanten können nun die Regelparameter für einen PID-Regler berechnet werden. Für Tn = T1 + T2 ergibts sich, dass Tn = 0,003 beträgt. Tv = (T1*T2)/Tn beträgt daher Tv = 9,67e-3. Damit beträgt der Proportionalfaktor der Regelung Kp = K*Tn = 0,27. Nun kann man über Kp und Tn den Integralteil der Regelung ermitteln. Dieser beträgt Ki = Kp/Tn = 90. Der D-Anteil des Reglers fällt, wie auch bei den Simulationsergebnissen mit MatLab sehr gering aus und wird mit 2,6109e-5 nicht weiter berücksichtigt. Es fällt auf, dass die simulierten und die berechneten Parameter sehr ähnlich sind. Die D-Anteile sind jeweils verschwindend gering. Die I-Anteile sind sehr groß und der Proportionalanteil ist klein. Aufgrund der vergleichbaren Ergebnisse zur Simulation wurden diese Parameter nicht weiter untersucht. Daher wurde im Weitern eine empirische Bestimmung der Regelparameter durchgeführt, um bessere Ergebnisse zu erzielen. 2.1.5 Empirische Bestimmung der Regelparameter Die empirische Bestimmung der Regelparameter ermöglicht es, den Regler auf das gegebene System fein einzustellen. Jeder Motor/Encoder weicht fertigungsbedingt oder durch Modellfehler vom Modellverhalten ab, weshalb eine Feinjustierung der Regelparameter der Systemidentifikation notwendig ist. Hierfür wurden die identifizierten Regelparameter aus 2.1.3.4 Ergebnisse „Robustes Regelverhalten“ verwendet und angepasst. Die auf diesem Wege empirisch ermittelten Regelparameter unterscheiden sich deutlich zu den Parametern aus 2.1.3.4, allerdings zeigt der Regler ein deutlich verbessertes Regelverhalten. Die Regelparameter wurden auf Kp = 0,75; Ki = 2,5; Kd = 0,005; ermittelt. 2.2 Gewählte Regelparameter Die empirisch ermittelten Regelparameter zeigen mit Abstand das beste Regelverhalten und kommen deshalb in unserem Projekt zum Einsatz. Reglerverhalten mit empirisch ermittelten Regelparametern In der Abbildung ist ersichtlich, wie nah die Regelung an der maximal möglichen Encoderauflösung arbeitet. Für eine genauere Regelung wird ein höher auflösender Encoder benötigt, da bei so einem agilen System, ein geringfügiges Schwingen um den Setpoint nicht verhindert werden kann. Das derzeitige System weist im schlimmsten Fall Setpoinabweichungen des Reglers von maximal 100 auf. Rechnet man diesen Fehler auf den Encoderausgang zurück, kann gezeigt werden, dass dieser Fehler einem Ändern des Encoderwertes um 5 entspricht. Dies bedeutet, wenn der Encoder seinen Ausgangswert um 5 verändert, führt dies zu einer Änderung am Reglerausgang von 100. Mit einer höheren Auflösung des Encoders könnte dieser Fehler deutlich reduziert werden. Der Regler schöpft das maximale Potenzial des dürftigen Encodersignals aus. 3. Video mit Ergebnissen |
| Mit Unterstützung von Prof. J. Walter | Sommersemester 2019 |
